Streaming Data and Entropy

• Streaming Data
  • Concept Drift
    • Tackling Drifting
  • Concept Evolution
  • Evaluation Criteria
• Data Processing
  • Instance Reduction
  • Dimensionality Reduction
  • Feature Space Simplification
• Entropy
  • Shannon Entropy
  • Generalized Entropy
    • Rényi Entropy
    • Tsallis Entropy
  • Comparison by Binominal Distribution
• References and Recommended Readings

Streaming Data

• Stream data, a potentially unbounded(infinite size), ever-growing dataset
  • Volume, Velocity (Variety)
    • Too large for single memory
    • Too fast for single CPU
    • Too changeable for single machine learning system

Concept Drift

• Concept drift, The nature of data may evolve over time due to various conditions
• The number and relevance of instances and features may change by drifting

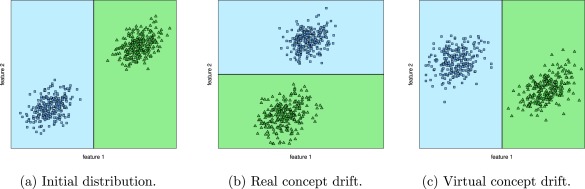
• Different influence on the learned classification boundaries
  • Real concept drift
  • Virtual concept drift

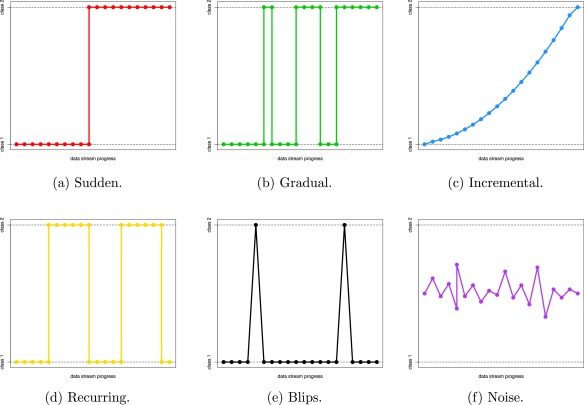
• Types of change
  • Sudden
  • Gradual
  • Incremental
  • Recurring
  • Blips
  • Noise
  • Mixed, more than one types

Tackling Drifting

• Concept drift detector
  • Explicit drift handling
  • Statistical criteria
    • SD
    • Predictive error
    • Instance distribution
    • Stability
  • Two stages
    • When drifting occurs, train a new classifier on recent instances
    • When drifting is severe, replace the old classifier with the new one
• Sliding windows
  • Implicit drift handling
  • Windows size is critical
• Online learner
  • Each object only be processed once
• Ensemble learner

Concept Evolution

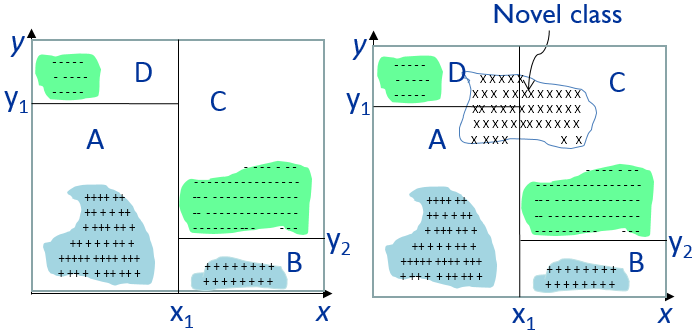
• New classes evolve in the data
• Solutions
  • Radius and adaptive threshold
  • Gini Coefficient
  • Multiple novel class detection

Evaluation Criteria

• Predictive power
• Memory consumption
• Recovery time
  • The time about accommodating new instances and updating algorithm structure
  • Process instances before new ones will arrive to avoid queuing
• Decision time
• Requirement for true class labels
  • Hard to label the entire data stream

Data Processing

Instance Reduction

• Sampling
• Instance Selection (IS)
  • New concept may be classified as noise and removed by a misbehavior
• Instance Generation (IG)

Dimensionality Reduction

• Feature Selection (FS)
  • Filter
    • Easily adaptable to the online environment
    • Hard to deal new features or classes
  • Wrapper
  • Hybrid
• Feature loss
  • Lossy Fixed (Lossy-F)
    • Fixed feature space
  • Lossy Local (Lossy-L)
    • Feature space varies with training batch
    • Feature space of training data may be different with test data
  • Lossless Homogenizing (Lossless)
    • Unify train/test feature space
    • Pad missing features

Feature Space Simplification

• Normalization
• Discretization
  • Bins
    • $\#$ bins
    • Size\boundaries of bins

Entropy

Shannon Entropy

$Hs(X) = - \sum_{i=1}^n p(x_i) \log_a(p(x_i))$

Generalized Entropy

• Control the tradeoff between contributions from the main mass of the distribution and the tail

$\langle X \rangle _{\phi} = \phi^{-1} (\sum_{i=1}^n p(x_i) \phi(x_i))$

Rényi Entropy

$\phi(x_i) = 2^{(1-\alpha)x_i}$

$H_{R\alpha}(X) = \frac{1}{1-\alpha}\log_a(\sum_{i=1}^n p(x_i)^{\alpha})$

$\lim_{\alpha \to 1}H_{R\alpha}(X) = Hs(X)$

Tsallis Entropy

$\phi(x_i) = \frac{2^{(1-\alpha)x_i}-1}{1-\alpha}$

$H_{T\alpha}(X) = \frac{1}{1-\alpha}(\sum_{i=1}^n p(x_i)^{\alpha} - 1)$

$\lim_{\alpha \to 1}H_{T\alpha}(X) = \log2Hs(X)$

Comparison by Binominal Distribution

• $p$, probability of success
• $1-p$, probability of failure

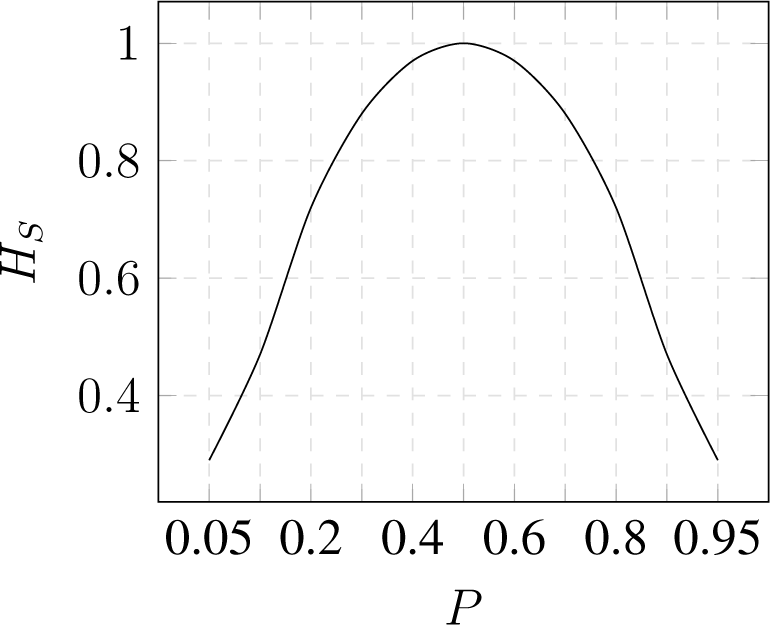
Shannon entropy

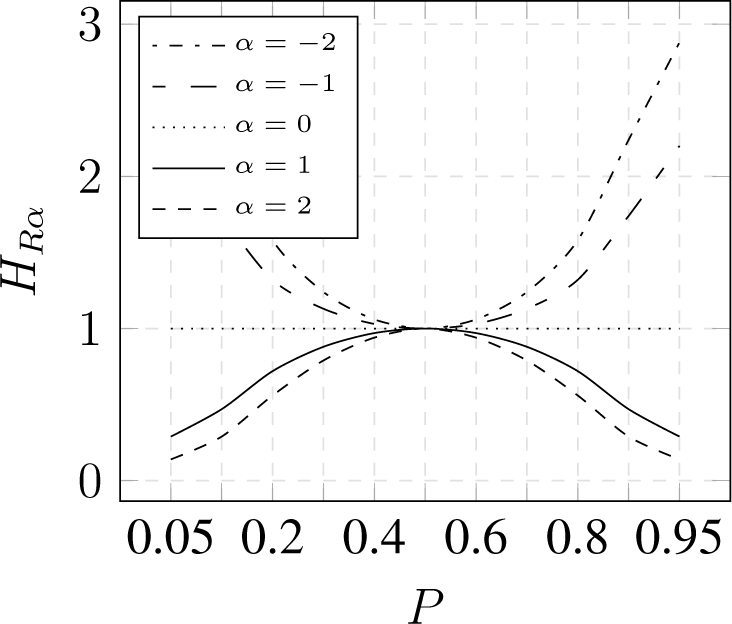
Rényi entropy of several $\alpha$-values

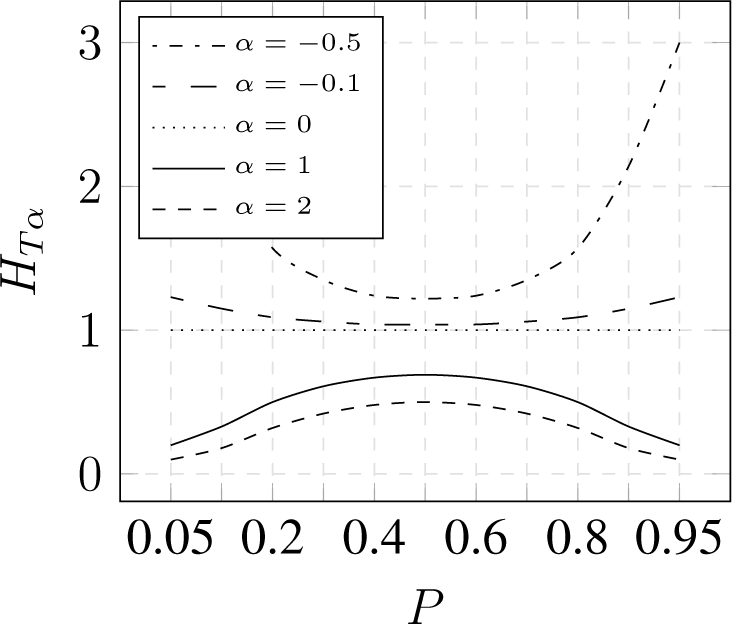
Tsallis entropy of several $\alpha$-values

References and Recommended Readings

• Data Stream Algorithms Intro, Sampling, Entropy
• Data Stream Mining
• A survey on data preprocessing for data stream mining: Current status and future directions
• Classification and Novel Class Detection of Data Streams in a Dynamic Feature Space
• Data Stream Mining, Data Mining and Knowledge Discovery Handbook
• An Entropy-Based Network Anomaly Detection Method
• Rényi entropy, wikipedia
• Shannon entropy in the context of machine learning and AI
• WELCOME TO THE ENTROPY ZOO, Beyond i.i.d. in information theory
• Philippe Faist, The Entropy Zoo